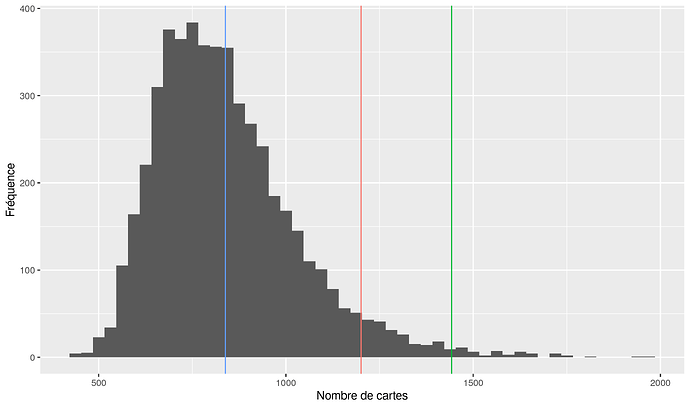
Deux petits graphiques pour attendre le déjeuner. Ils sont issus de simulations. Dans le premier, on retrouve nos 150 cartes achetées une par une. J’ai simulé 5000 séquences d’achat et j’ai représenté la fréquence de chaque nombre d’achats. Les lignes verticales correspondent aux valeurs théoriques : moyenne, 95% de chance et 99% de chance. Ça colle parfaitement 
On voit que la distribution n’est pas gaussienne en raison d’une longue traîne (en exp(-ax) au lieu de exp(-ax^2) pour l’aspect technique). D’ailleurs mon histoire sur le théorème centrale limite est un peu foireuse car il faut appliquer une version très étendue du théorème et je ne suis pas sûr que les conditions techniques soient remplies…
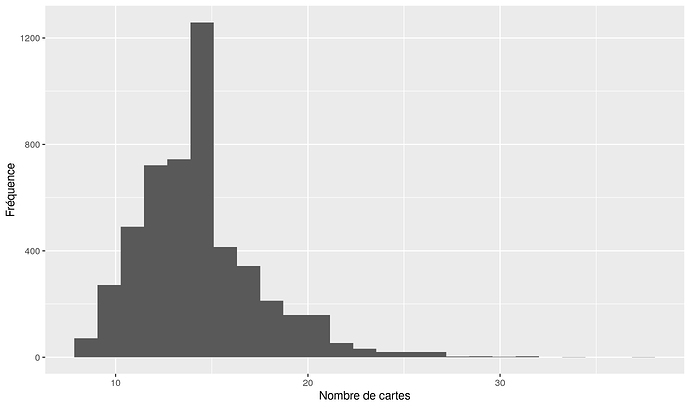
Le deuxième graphique est une simulation qui se rapproche de la situation de Chronica universalis avec 150 cartes mais des paquets de 50. Évidemment, on achète beaucoup moins de paquets, beaucoup moins que la valeur de 50 pourrait le laisser croire. En effet quand j’achète 50 fois une carte unique, j’ai de grosses chances d’avoir des doublons, alors que par définition, un paquet de 50 n’en contient pas. Ici, on achète en moyenne (et en médiane) autour de 14 paquets, ce qui veut dire 700 cartes, contre 842 avec les achats uniques. Pour atteindre une certitude de 99%, on doit acheter 25 paquets, soit donc 1250 cartes contre 1442.
Dès que j’ai le temps, je vous décortique la formule théorique pour le cas des achats par paquets. Notez que la simulation indique déjà que ça peut revenir cher