Comme on est quelques profs de maths ici et que les jeux posent de très intéressantes questions de maths, pourquoi ne pas regrouper ici toutes les discussions barbantes passionnantes sur ce sujet, hein, pourquoi ne pas ?
le noble art des maths.
Et donc je commence au sujet des questions posées par Chronica universalis.
Le problème soulevé dans le cadre de la discussion sur Chronica Universalis est connu en maths comme celui du collectionneur de vignettes (coupon collector en anglais).
C’est un problème bien connu et bien étudié dans ses versions simples. On trouve sur le site du CNRS un article relativement facile d’accès sur le sujet pour les personnes avec une certaine aisance en mathématique.
Je vous fais un résumé du cas le plus simple car le raisonnement l’est aussi. On suppose que la collection comprend au total n cartes différentes. On suppose que les cartes sont achetées une par une et qu’elles sont équiprobables, ce qui veut dire que chaque carte à 1/n chance d’être celle qu’on achète : on prend une carte parmi n, d’où le 1 divisé par n.
Pour la première carte achetée, on est bien sûr certain d’avoir une nouvelle carte. Quand on possède p cartes, la probabilité d’obtenir une nouvelle carte tombe à (n-p)/n, grâce à l’hypothèse d’uniformité. En effet, sur les n cartes, j’en possède déjà p, donc il ne reste que n-p cartes intéressantes. Parmi les n tirages possibles, seuls n-p m’intéressent, d’où la probabilité (n-p)/n (qui vient toujours de l’hypothèse d’équiprobabilité).
Pour étudier le problème, on introduit des variables aléatoires (ce n’est pas sale). Ce sont des quantités aléatoires auxquelles on donne un nom, pour simplifier. X1 est le nombre de cartes que j’achète pour passer de 0 carte à 1 carte (on sait que X1=1, ce n’est pas une variable aléatoire dans les faits). X2 est le nombre de cartes que j’achète pour passer de 1 carte à 2 cartes distinctes, etc. Par exemple Xk est le nombre de cartes que j’achète pour passer de k-1 cartes distinctes à k cartes distinctes.
X2 est bien une quantité aléatoire car j’ai une probabilité de (n-1)/n de passer de 1 à 2 en un achat, mais il me reste une probabilité de 1/n de rester avec une seule carte après mon achat. X2 (et ses copines) sont des variables géométriques et on connaît bien leur comportement : la probabilité que Xk soit égale à p, P(Xk=p), vaut (k-1)^(p-1)(n-k+1)/(n^p) (je note a^b pour a à la puissance b). La formule s’explique bien : il vaut que je me rate (p-1) fois puis que je réussisse. Comme les achats sont indépendants, je multiplie les probabilités. Chaque ratage a une probabilité de (k-1)/n (je retombe sur une de mes k-1 cartes) alors que la réussite a une probabilité de (n-k+1)/n.
Un truc bien pratique est que la valeur moyenne de Xk est tout simplement n/(n-k-1). Un autre truc bien pratique est que pour obtenir une collection complète, je dois acheter X1+X2+…+Xk+…+Xn cartes (d’après la définition). Un dernier truc pratique est que la valeur moyenne d’une somme de variables aléatoires est la somme de leur valeurs moyennes. En moyenne, je dois donc acheter 1+n/(n-1)+n/(n-2)+…+n/(n-k+1)+…+n cartes. Cela peut s’écrire n(1+1/2+1/3+…+1/n). La somme 1+1/2+1/3+…+1/n est Hn le n-ème nombre harmonique, un truc qui plaît bien aux matheux. On sait en particulier approcher l’objet et dire que Hn vaut environ ln n + 0.5772156649.
Donc en moyenne, il faut acheter n(ln n + 0.5772156649) paquets pour obtenir une collection complète. Donc pour 150 cartes, on est sur environ 838 cartes (et pas 752 comme j’avais écrit ailleurs en oubliant le 0.58).
Voilà pour la version facile. On peut dire de nombreuses autres choses en s’appuyant sur le fait que les variables sont indépendantes. De ce fait la variance du nombre de cartes est la somme des variantes des différentes variables aléatoires. La variance de Xk vaut (1-lk)/(lk^2) avec lk=(n-k+1)/n. Avec quelques manipulations, on peut montrer que la variance est plus petite que pi^2n^2/6 (oui, oui, le pi des cercles). Pour 150 cartes, ça nous fait une variance de 37011 (!!!) et donc un écart type de 192. Attention, ce n’est pas une distribution gaussienne, donc on ne peut pas en déduire que dans 95% des cas on aura entre 838-2192=454 et 838+2192=1222 cartes à acheter, mais ça donne une idée de la variabilité assez importante à laquelle on est confronté.
En s’appuyant sur la variance ou sur d’autres approches plus précises, on peut estimer la concentration du nombre de paquet autour de la valeur moyenne d’une façon plus raisonnable que mon calcul gaussien au dessus. Par exemple pour être sûr à 95% d’avoir une collection complète, il faut acheter environ 1201 cartes (comme quoi l’approximation gaussienne n’est pas si mauvaise). La formule n’est pas super compliquée : si on être sûr avec une probabilité de 1-delta, il faut (1-log delta/log n) n log n achats.
Malheureusement, les choses se compliquent considérablement quand on achète des paquets de cartes. La suite au prochain numéro…
ca, c’est la raison pour laquelle je prefere les LCGs.
Pour le moment, tes cartes sont eauiprobables. Rajoute la dedans les uncos, rares et mythiques et on comprend le succes de Wizards of the Coast.
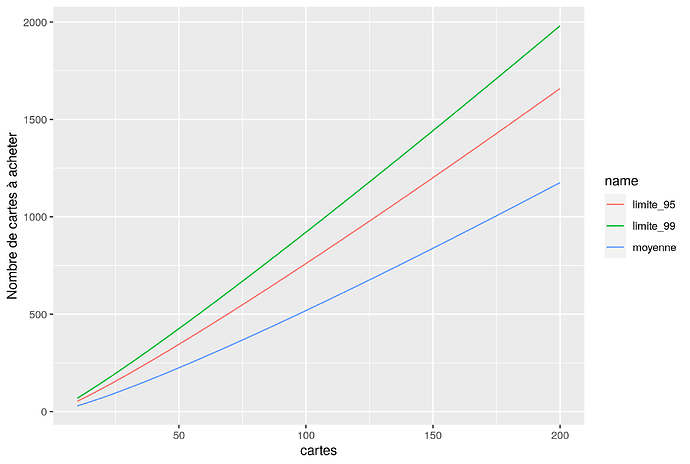
Petite illustration graphique du comportement des choses. D’abord le nombre de cartes à acheter en fonction du nombre total de cartes, avec le nombre moyen, celui pour avoir une certitude à 95% et celui pour une certitude à 99%.
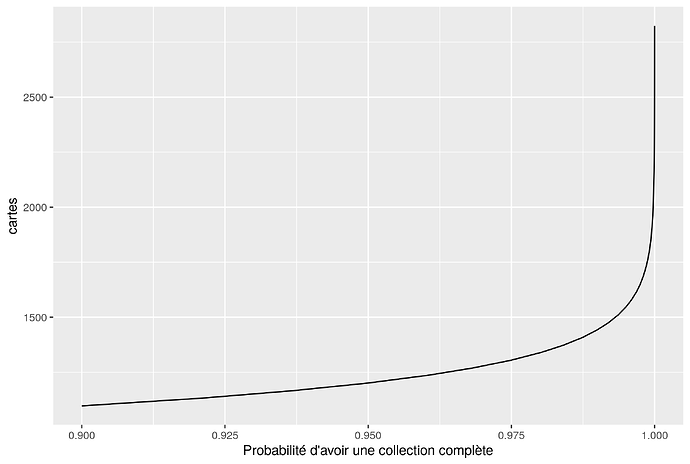
Ensuite le comportement pour 150 cartes. Combien faut-il acheter de cartes pour faire tendre la probabilité d’avoir une collection complète vers 100%. On voit que ça explose quand on se rapproche de 100%, sachant que ça vaut effectivement l’infini pour exactement 100%
Merci pour ce post bien sympa. Moi aussi je conseille toujours à mes étudiants d’évaluer les choses selon une gaussienne, même si ce n’est pas rigoureux pour avoir au moins une idée.
Pour être honnête, je suis toujours surpris quand ça marche, mais ici c’est normal (ah, ah, super jeu de mots) : comme on somme des variables indépendantes, ça se comporte asymptotiquement comme une gaussienne selon le théorème central limite. Donc avec beaucoup de cartes (n grand), c’est effectivement une gaussienne.
Alors j’ai pas tout compris mais j’en conclus qu’il vaut mieux se contenter des cartes sur lesquelles on tombe pour jouer tranquillement ! 
Ou compter sur les échanges, mais je ne vais pas relancer le débat ! 
Les échanges s’analysent pas trop mal pour le cas simple et sont extrêmement puissants. En gros, quand on a un grand nombre de cartes (n), il suffit d’acheter n log n cartes plus un complément de l’ordre de (q-1) n log log n cartes pour q personnes qui font des échanges optimaux. L’astuce est que n log log n augmente relativement lentement. Par exemple pour n=150, ça fait 241, à comparer à 751 pour n log n. Donc à 2 personnes, par exemple, il faut acheter en moyenne de l’ordre de 1000 cartes au lieu de 838 tout seul (et donc 1676 au total !).
L’intuition est que si j’achète de l’ordre de n log n cartes pour en avoir n, il m’en reste en gros n (log n -1) qui devraient être réparties plus ou moins équitablement. Donc avec 838 cartes, j’en ai quand même presque 700 en rab. De quoi faire d’autres collections avec seulement quelques cartes qui manquent…
Si je puis me permettre d’intervenir dans cette discussion alors que je ne suis pas prof de maths, je voudrais suggérer que vous abordiez (p-e dans une autre discussion vu comment celle-ci part et que peut-être que cela en rebuterait plusieurs de suivre un fil de discussion avec de tels messages voir qu’ils décrocheraient avant de voir les sujets qui pourraient les intéresser) des sujets plus ouverts au commun des joueurs et des précisions pour des jeux, voir avec de l’explication simple pour les jeunes ou ceux qui ont du mal avec les maths, histoire qu’ils puissent s’ouvrir au sujet des maths dans les jeux ;p
Par exemple, une première question simple pour cette discussion mais qui n’est pas évidente pour tout le monde :
Vaut-il mieux un jet à 4+ ou un jet à 5+ relançable? (par exemple à Zombicide: pour un choix d’armure à 5+ avec relance grâce à un bouclier ou simplement la 4+ du bouclier)
Spoiler pour ceux que cela intéresse mais qui ne suivront plus le fil de discussion et qui l'ignoreraient
La réponse est : 5+ relançable car la probabilité de réussir est légèrement supérieure à la 4+ (histoire de proba « toussa toussa » le vieil oncle malade  je laisse qui veut l’expliquer si jamais il y a des motivés)
je laisse qui veut l’expliquer si jamais il y a des motivés)
C’est compliqué de différencier les problèmes et de les classer en accessibles ou non accessibles. Je trouve d’ailleurs justement que l’explication du premier post est simplifiée, et assez explicite sur certains points (sur d’autres il faudrait grandement rentrer dans les détails pour être plus explicite).
Et pour ton problème de Zombicide, ce n’est en effet pas très compliqué. Je ne connais pas la règle donc je vais juste supposer que le 5+ relançable ne se relance qu’une fois. La proba de 4+ est de 1/2 (ou 3/6) sur un dé équilibré, vu que sur les 6 possibilités de résultats du dé, il y en a 3 qui expriment un succès. Pour le 5+relançable, on a une proba de réussite de 1/3 (ou 2/6), à laquelle il faut ajouter la proba de réussite au deuxième jet. Celle-ci vaut 4/6 * 2/6 (4/6 car on a échoué au premier lancer si on relance le dé, et 2/6 pour la même raison qu’avant).
On a donc au final 3/6, ou 18/36 pour le lancer 4+, et 2/6 + 4/6 * 2/6 = 12/36 + 8/36 = 20/36 pour le lancer à 5+ relançable.
Excellente idée de sujet !
Le sujet de mes rêves 
Faudrait demander à @thierry d’installer MathJax sur le forum pour pouvoir écrire les formules en Latex 
Je vois que @ran-cadren est dans la team R donc ça va on peut continuer à discuter 
J’avoue que ce serait plus facile avec Latex, mais ça doit lui coûter à Thierry pour juste 3 peï comme nous qui allons l’utiliser…
+1
« yaka »
Ah punaise, si on peut avoir le plugin latex/mathjax, ça va être très très bien. Surtout pour la suite de l’analyse du problème de vignettes.
Concernant les relances et compagnie, il y a une analyse assez détaillée du cas de Conan ici : première partie et deuxième partie.
team ggplot et tidyverse ![]()
Un problème de logique sur la problématique de « connaissance commune » que j’adore :
https://xkcd.com/blue_eyes.html
Y a de quoi se faire des noeuds au cerveau.
Tu bosses chez Sorare et tu essaies de convaincre les pigeons gens que les vignettes virtuelles c’est le top ? 
Merci beaucoup @ran-cadren , c’est pour l’instant très clair !
J’attends la suite de la démonstration avec impatience et, vraiment, intérêt !
Et merci du temps que tu prends pour détailler, c’est utile…